北京市奥校精选试题及答案95(2)

　　二年级

　　1.找规律填数：3、28、6、26、9、24、（）、22、15、（）、（）

　　解答：奇数项依次加3，偶数项依次减2。填12、20、18。

　　2.找规律填数：35、2、30、4、25、6、（）、（）、15、10、（）

　　解答：奇数项依次减5，偶数项依次加2。填20、8、10。

　　三年级

　　1.观察下面已给出的数表，并按规律填空

　　1

　　2  4

　　3  7  11

　　4  10  16  22

　　5  13  21  （  ）  37

　　6  16  （  ）   36  46  56

     解答：

　　1

　　2  4

　　3  7  11

　　4  10  16  22

　　5  13  21  （ 29 ）  37

　　6  16  （ 26 ）   36  46  56

　　2.小明有1角、5角的硬币共35枚，一共9元5角，1角、5角硬币各有几枚？

　　解答：9元5角=95（角）

　　1×35=35（角）

　　95-35=60（角）

　　60÷(5-1)=15（枚）—5角的

　　35-15=20（枚）—1角的

　　四年级

　　1.观察数组(1,2,3),(3,4,5),(5,6,7),(7,8,9)的规律，求：

　　(1)第20组中的三个数的和。

　　(2)前20组中所有数的和。

　　解答：(1)观察可知，每n组的中间数是2×n，所以第20组三个数的和为2×30×3=120

　　(2)前20组所有数的和：2×(1+2+3+……+20)×3=1260

　　2.一个数列的第一项是1，之后的每一项是这样得到的：如果前一项是一位数，接着的一项就等于前一项的两倍，如果前一项是两位数，接着的一项就等于前一项个位数字的两倍，请问：

　　(1)第100项是多少？

　　(2)前一百项的和是多少？

　　解答：(1)按题目规律列举如下：

　　1,2,4,8,16,12,4,……可知4,8,16,12为一周期

　　(100-2)÷4=24余2，所以第100项是8

　　(2)由(1)可知，4,8,16,12之和为40，且共有24项。

　　所以前100项之和为1+2+24×40+4+8=975

　　五年级

　　1.求0.000……01（小数点后共有2009个0）的平方其结果的小数点后有多少个0？

　　解答：结果共有（2009＋1）×2=4020位小数，小数点后的0共有4020－1=4019个。

　　2.把5本不同的数学书，放入两个不同的书包里，使得每个书包内至少有一本书。有多少种不同放法？

　　解答：每一本书均有两种选择，根据乘法原理共有2×2×2×2×2=32种情况，而其中有两种情况是都放进同一个书包的，所以答案应该是32－2=30种。

　　六年级

　　1.将前9个奇数放在3×3的方格中，并且使横向、纵向和对角线方向数字和相等。问A＋E是多少？

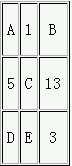
　　解答：9个奇数之和为81，81÷3=27，C=27－5－13=9，E=27－1－9=17，A=27－3－9=15，A＋E=32

　　2.二十多位小朋友围成一圈做游戏，他们依顺时针顺序从小赵报1开始连续报数，但7的倍数或带有数字7的数都要跳过去不报，报错的人表演一个节目，小明是第一个报错的人，当他右边的同学报90时，他错报了91，如果他第一次报数报的是19，那么这群小朋友共有多少人？

　　解答：19—91共有24个数不能报，当小明报91时，应是报19后的第91－19－24=48个数，这时以小明为起点刚好为完整的若干圈，48的约数中在20至30之间的数只有24，所以这群小朋友有24个人。