北京市奥校精选试题及答案119(2)

　　二年级

　　1.有一列数：1、2、3、4、5、6、……

　　（1）7—60有多少个双数？有多少个单数？

　　（2）从18—74有多少个双数？有多少个单数？

　　解答：（1）有27个双数，有27个单数。

　　（2）有29个双数，有28个单数。

　　2.数一数，有多少个正方形？

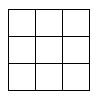
　　解答：图中的正方形可以分为小、中、大三类。第一类小的正方形有9个，第二类中等大小的（由4个小正方形组成）有4个，第三类大的有1个。共有14个。

　　三年级

　　1.下面的算式中0—9各用了一次，现在已经写出三个数字，请把其它的补上。

　　解答：改写成加法算式后有些数字可以直接确定。百位相加最多为12，所以只能为10，而十位一定会向百位进位，所以百位和千位的数字可以确定。

　　这时算式变为，还剩3、4、5、9没填。

　　个位可以填3、9或9、5。通过十位判断只能填9、5，十位填4、3。最后改为减法算式为1035－789=246。

　　2.班主任给同学们排座位，每排都恰好有3名男生4名女生。如果女生一共有32名，那么有多少名男生？

　　解答：32÷4=8（排）8×3=24（名）

　　四年级

　　1.下面的算式中0—9各用了一次，现在已经写出三个数字，请把其它的补上。

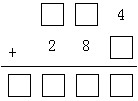
　　解答：千位只能是1，而百位相加最多为12，因此结果的百位只能为0，十位一定会向百位进位，因此百位一定填7。

　　这时算式变为，还剩3、5、6、9没填。

　　个位只能填5、9或9、3。如果填5、9，显然十位没法填。如果填9、3，十位可以填6、5，因此算式为764＋289=1053。

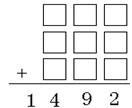
　　2.1492年，哥伦布率领船队“发现”了新大陆。到达新大陆的当晚，他们举行盛大的庆祝活动，在宴会最热闹的时候，哥伦布举杯说道：“今年是1492年，我们要永远记住这个数字，我现在给大家出一道和1492有关的数学题，谁能答出来，就会获得丰厚的奖赏。”哥伦布的问题是这样的：把下图中的竖式填完整，使得填入的数字和最大，答对的船员会得到与这个最大值数量相同的金币。最后，一个聪明的船员拿到了金币。你知道这个聪明的船员拿了多少金币吗？

　　五年级

　　1.大于60000的“上升数”有多少个？（“上升数”指相邻两个数位中要求右边数字比左边的大）

　　解答：五位的“上升数”最大为56789，因此按条目要求至少为六位数。

　　解答：要想填入的数字和最大，每一位上都应该有进位，个位、十位每一位都向前2个进位，百位向前一个进位：5×9+1+4+9+2=61，所以船员拿了61个金币。

　　五年级

　　1.大于60000的“上升数”有多少个？（“上升数”指相邻两个数位中要求右边数字比左边的大）

　　解答：五位的“上升数”最大为56789，因此按条目要求至少为六位数。

    2.各数位上数码之和是15的三位数共有多少个？

　　解答：如果首位为1，那么后两位可以是59、68、77、86、95，5种。

　　如果首位为2，那么后两位可以是49、58、……、94，6种。

　　……

　　如果首位为5，那么后两位可以是19、28、……、91，9种。

　　如果首位为6，那么后两位可以是09、18、……、90，10种。

　　如果首位为7，那么后两位可以是08、17、……、80，9种。

　　……

　　如果首位为9，那么后两位可以是06、15、……、60，7种。

　　共有5＋6＋……＋9＋10＋9＋8＋7=69。

　　六年级

　　1.一个三位数与他的各个数位之和是182，求这个三位数。

　　2.有A、B两组数，每组数都按一定的规律排列着，并且每组都各有25个数。A组数中前几个是这样排列的1，6，11，16，21……；B组数中最后几个是这样排列的……，105，110，115，120，125。那么，A、B这两组数中所有数的和是多少？

　　解答：首先通过观察容易发现A、B两组数的排列规律。这两组数都排成等差数列，并且每组数都有25个数。用等差数列的求和公式可以算出结果，但必须先推算出A组数的第25个及B组数的第1个。如果同学们能从“两组数个数相等”与“两组数都是公差为5的等差数列”这两个条件入手，用首尾配对的技巧来解，那么计算简便多了。（1＋125）×25=3150