北京市奥校精选试题及答案120(2)

　　二年级

　　1.有一列数：1,2,3,4,5,6……

　　（1）13-65之间有多少个数？

　　（2）17-59之间有多少个双数？有多少个单数？

　　解答：（1）64－13=51（个）

　　（2）17-59之间有58－17=41个数，其中有21个双数，20个单数。

　　2.有一个长方形，用两条直线最多可以将长方形分成几部分？

　　解答：一条直线可以分成两部分，第二条直线可以将原来每个部分再分成两部分，所以一共可以分成4部分。

　　三年级

　　1.如图，○、□、△分别代表不同的数字，那么它们分别代表什么？

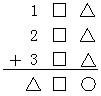
　　解答：个位一定往十位进位1或者2，那么通过十位判断，□只能为4或9，个位往十位一定进2。再看百位，这时△可以是7或8。当△=7时，○=1，□=4；当△=8时，○=4，□=9。

　　2.体育课上，老师让42名同学排成一行，A发现有一半的人站在自己左边，B发现自己是从右往左数的第12个，那么A和B之间有多少名同学？

　　解答：A左边有21名同学，B左边有11名同学，加上A、B两名同学，一共有21＋11＋2=34名同学，A和B之间有42－34=8名同学。

　　四年级

　　1.在下面的竖式中，相同的汉字代表相同的数字，不同的汉字代表不同的数字，每个汉字分别代表什么数字？

　　解答：“数”是突破口，“数”=1。通过个位看出来“用”一定是偶数，所以只能为8，“学”=2，“为”=4，“好”=6。

　　2.在下面的空格内分别填入适当的数字，可以使竖式成立，所填的七个数字之和最大是多少？

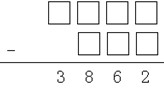
　　解答：要想使七个数的和最大，每一个数都应该尽可能的大，是4899-937=3862，因此七个数的和最大是51。

　　五年级

　　1.高速公路入口处的收费站有1号、2号、3号、4号共四个开放的收费窗口，有A、B、C三辆轿车要通过窗口购票进入高速公路。那么这三辆轿车共有多少种不同的购票次序？（同一窗口有两辆车时，按照A在最前、C在最后的顺序通过）

　　解答：每辆车都有4个窗口可以选。根据题目最后的说明可知，如果两辆车选择了同一窗口，那么一定按照AB、AC、BC的顺序通过；如果三辆车选择了同一窗口，一定按照ABC的顺序通过。因此共有4×4×4=64种。

　　2.小于2000的四位数中数字和等于24的数共有多少个？

　　解答：这样的四位数千位一定是1，后三位的和为23=9＋9＋5=9＋8＋6=9＋7＋7=8＋8＋7，共有3＋3!＋3＋3=15种。

　　六年级

　　1.有2角，5角和1元的纸制人民币共20张，共计12元，每种纸币至少一张。则每种纸币分别有多少张？

　　解答：设三种纸币各有x、y、z张（x、y、z均不小于1）

　　2x+5y+10z=120

　　x+y+z=20

　　可知x为5的倍数，可以解得x=5,y=8,z=7

　　2.在左边的乘法算式中，我、学、数、乐各代表四个不相同的数字。如果“乐”代表“9”，那么，“我”、“数”、“学”分别代表多少？

　　解答：由“乐”代表9，可推到“学”代表1，“数”代表6。积是一个十位数，并且前两位数都是6，因为800002＜6661661161＜900002，所以8≤我≤9，显然，“我”只能是8。