北京市奥校精选试题及答案160

　　以下是北京市奥校内部试题，每套试题附有答案及详解。小升初目标校为东城区5中、2中的同学们要尤其注意此套试题。

　　二年级

　　1. 妈妈买来大米2袋，面粉4袋，共重200千克，已知1袋大米的重量和2袋面粉的重量相等，那么一袋大米重（     ）千克。

　　解答：2米＋4面=200

　　1米=2面

　　1米=（     ）千克

　　二式代入一式，2面＋2面＋4面=200，面=25

　　2. 百货商店运来300双球鞋，分别装在2个大木箱、6个纸箱里。如果2个纸箱同1个木箱装的球鞋一样多，那么每个木箱可装（    ）双球鞋，每个纸箱可装（    ）双球鞋。

　　解答：2木＋6纸=300

　　2纸=1木

　　得：2纸＋2纸＋6纸=300。所以，每个纸箱可装30双球鞋。每个木箱可装2×30=60（双）

　　三年级

　　1.   一队学生站成20行20列方阵，如果去掉4行4列，那么要减少多少人？

　　解答：20－4=16（人），20×20=400（人），16×16=256（人），400－256=144（人）

　　2. 有黑白两种棋子共300枚，按每堆3枚分成100堆。其中只有1枚白子的共27堆，有2枚或3枚黑子的共42堆，有3枚白子的与有3枚黑子的堆数相等。那么在全部棋子中，白子共有多少枚？

　　解答：27×1+43×2+15×3=158（枚）

　　四年级

　　1. 甲村、乙村相距6千米，小张和小王分别从甲、乙两村同时出发，在两村之间往返行走（到达另一村后就马上折回）。在出发40分钟后两人第一次相遇，小王到达甲村后返回，在离甲村2千米处两人第二次相遇。小张和小王的速度各是多少？

　　解答：两次相遇共走3个全程，所用时间是3个40分钟，即2个小时：

　　40×3=120（分）=2（时）

　　从出发到第二次相遇小张走了6×2-2=10（千米），小王走了6+2=8（千米），因此小张的速度10÷2=5（千米），小王的速度8÷2=4（千米）。

　　2. 甲乙两车同时从A地出发，不停的往返于A,B两地之间。已知甲车的速度比乙车快，并且两车出发后第一次和第二次相遇都在途中C地。甲车的速度是乙车的几倍？

　　解答：2倍。

　　每次相遇都共行一个来回，所用的时间相等，因此两次相遇时，甲车所走的路程也是相等的。第一次相遇时甲走AC+2BC，第二次相遇时甲走2AC，所以AC+2BC=2AC，因此AC=2BC。时间相同的情况下，路程是2倍的关系，速度也是2倍的关系。

　　五年级

　　1、一张四边形纸上共有23个点，如果把四边形的顶点算在一起，则一共有27个点。已知这些点中的任意三个点都不在同一条直线上。按下面的规定把这张纸剪成一些三角形：（1）每个三角形的顶点都是这27个点中的3个；（2）每个三角形内都不再有这些点。那么这张四边形纸共可以剪出多少个三角形？

　　解答：四边形纸上共有23个点，如果直接考虑可以剪出多少个三角形，会感到无从入手，所以我们应从简单处想起。

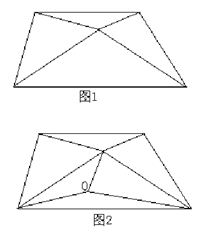
　　首先考虑纸上有一个点时可以剪出多少个三角形，这是非常简单的问题（  如图1），可以剪出4个三角形。然后考虑在纸上再增加一个点O，由于没 有三个点在一条直线上，所以A点只能在某一个三角形内部（如图2）能剪出的三角形增加了2个。再进一步考虑增加点数，可以验证这一结论是正确的。这样对于简单问题的分析，我们总结出了规律：四边形纸上有一个点时可以剪出4个三角形，以后每增加一个点就增加2个三角形。

　　4＋2×（23－1）=48（个）

　　所以这张四边形纸共可以剪出48个三角形。

　　2、某城市的街道非常整齐(如图),从西南角A处走到对角线DB处,共有多少种不同的走法?

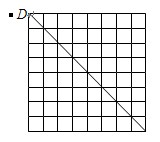
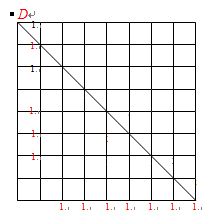
    　解答：用标数法计算对对角线BD上的每一个交叉点的走法总数,如图依次是1,8,28,56,70,56,28,8,1.由加法原理知,一共有1+8+28+56+70+56+28+8+1=256(种)不同的走法.

   六年级

　　1. 如图，正方体的棱长为6厘米，连接正方体其中六条棱的中点形成一个正六边形，而连接其中三个顶点形成一个三角形。正方体夹在六边形与三角形之间的立体图形的体积是多少立方厘米？

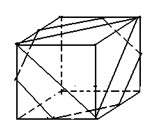
　　解答：1/2×[6×6×6—2×（1/3×1/2×6×6×6）]=72（立方厘米）

　　2. 将25个同样的零件分别放在5只同样的箱子中，要求有人要1～25个之间的任意多个零件时，都可以不拆箱地从中拿出若干箱如数付给他。这5箱有多少种不同方法？

　　解答：前三箱是1、2、4时后2箱是8，10或7，11或6，12或5，13；前三箱是1，2，3时后2箱是7，12或6，13。所以共有6种不同方法。