北京市奥校精选试题及答案169

　　以下是北京市奥校内部试题，每套试题附有答案及详解。小升初目标校为东城区5中、2中的同学们要尤其注意此套试题。

　　二年级

　　1、有一本书共200，页码依次为1、2、3、……、199、200，问数字 “1”在页码中共出现了多少次？

　　答案：140（次）

    2.

　　解答：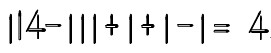

　　三年级

　　1、A、B、C之和是65，A比B大5，B比C大9，A是（   ）。

　　解答：28

　　2、 下面有三个加法等式，当正方形、三角形、圆形符号各代表什么数时，才能使等式成立。□是（    ），△是（     ），○是（      ）。

　　□    +□+△+○＝16

　　□    +△+△+○＝13

　　□    +△+○+○＝11

　　解答：6，3，1

　　四年级

　　1、100名男女运动员参加乒乓球单打淘汰赛，要产生男女冠军各一名，则要安排单打赛多少场？（   ）

　　解答： 98

　　2、某机关打算在系统内举办篮球比赛，采用单循环赛制，根据时间安排，只能进行21场比赛，请问最多能有几个代表队参赛？（     ）

　　解答：7

　　五年级

　　1. 有一些完全平方数的最后三位数码都相同且不为0，那么这些数中最小的是多少？

　　解答：一个完全平方数的末尾数只能是0，1，4，5，6，9。当其末位数为1，4，5，9时，其十位数必须是偶数；当其末位数为6时，其十位数必须是奇数。所以当完全平方数的末三位数码都相同时，这三位数码只能是444，而444又不是完全平方数，所以最小的完全平方数是1444。

　　2. 小林从A地出发步行往B地，同时小明从B地出发骑车往A地走的是同一条路，1个小时后两人在途中相遇。小明到达A地后立即返回，在第一次相遇后又经过40分钟，小明在途中追上小林。小明到达B地后又立即返回，那么他们第三次相遇的地点到A 、B两地的距离之比是多少？

　　解答：第一次相遇到第二次相遇之间，小明行驶40分钟的距离小林要步行160分钟，所以小明的速度是小林的4倍，AB之间距离小林需要步行5小时。第三次相遇时，小林和小明所走的路程之和是AB之距离的3倍。他们走过的路程之和为AB的距离时，用了1小时，所以第三次相遇时小林共步行了3小时，故第三次相遇点与AB地的距离比是3：2。

　　六年级

　　1、 下图的圆周上放置有3000枚棋子，按顺时针依次编号为1，2，3，…，2999，3000。首先取走3号棋子，然后按顺时针方向，每隔2枚棋子就取走1枚棋子，…，直到1号棋子被取走为止。问：此时，（1）圆周上还有多少枚棋子?（2）在圆周上剩下的棋子中，从编号最小一枚棋子开始数，第181枚棋子的编号是多少？

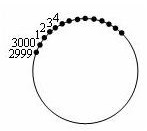
    解答：第一圈刚好把能被3整除的取走，即第一圈最后取走编号为3000的，共取走1000枚，剩下2000枚，此时1号仍为第一个。再从这2000枚棋子中隔2隔取走1个，第二圈最后取走的是2000枚中的第1998枚，共取走666枚，第1999、2000枚没有取走。再取就是第1号了，取走第1号时1000＋666＋1＝1667枚棋子，还剩下1333枚棋子。

　　将第一圈取走的用绿色表示，将第二圈取走的用红色数字表示：

　　1，2，3，4，5，6，7，8，9，10，11，12，13，14，15，16，17，18，19，20，21，

　　22，23，24，……

　　可见，每18个一循环，18个数去掉10个，剩下8个。拿走1后，剩下的最小编号是2，从2数第181枚，就是从1数第182枚。182÷8＝22余6，22×18＝396。

    将366以后的数排列出来，并根据上述分析标上颜色：

　　397，398，399，400，401，402，403，404，405，406，407，408，409，……

　　可见，剩下的第6个数是407，即取走1号棋子后，从剩下的最小号数，第181枚棋子的编号是407。

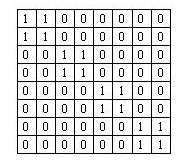
　　2、 在8×8的方格网填入不同的自然数，使每个方格里都只有一个数，如果一个方格里的数，大于它所在的行中至少6个方格内的数，并且大于它所在的列中至少6个方格内的数，则称这个方格为“好格”。那么，“好格”最多有___个.

　　解答：因为一行有8个数，至多有2个数可以大于同行的6个数，只有当这两个数分别同时大于所在列的6个数时，这个格才是“好格”，所以一行最多有两个“好格”，8行最多有2×8＝16个“好格”。16个“好格”是可能的，下面给出一个例子，图中标“1”的16个格子是“好格”。