北京市奥校精选试题及答案197

　　以下是北京市奥校内部试题，每套试题附有答案及详解。小升初目标校为东城区5中、2中的同学们要尤其注意此套试题。

　　二年级

　　1．商店规定3个空汽水瓶可以换一瓶汽水，小明买了10瓶汽水，喝完后用空瓶去换汽水，他一共可以喝到多少瓶汽水？

　　解：他可以喝到15瓶汽水。

　　2．19名战士要过河，河边只有一条船，每次只能运4名战士，至少需要多少次，才能使全体战士过河？

　　解：19÷4=4（次）…3（人）   4+1=5（次）

　　三年级

　　1. 求1—100的自然数中，不是7的倍数的所有自然数的总和。

　　分析与解答：1—100的所有自然数的和是5050，其中包括两大部分：不是7的倍数和与所有7的倍数和两类。7的倍数为7，14，21，……91，98。这是一个等差数列，一共14项：

　　解： 98÷7=14，

　　总和为：（7+98）×14÷2=735

　　不是7的倍数和为：5050-735=4315

　　2. 如图，数表中的上、下两行都是等差数列，那么同一列中两个数的差（大数减小数）最小是多少？

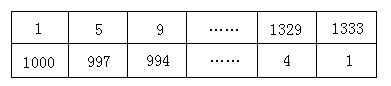
　　分析与解答：

　　从左向右算，大数减小数是下-上，它们的差分别为：999、992、985、……这是一个等差数列，公差为7，除以7余数相同均为5，所以最小值为5，共有（999-5）÷7+1=143项；第143项的大数为： 1000-（143-1）×3=574，小的数为：1+（143-1）×4=569，574-569=5.

　　从右向左算，大数减小数是上-下，它们的差分别为：1332、1325、1318、……这是一个等差数列，公差为7，除以7余数相同均为2，所以最小值为2，共有（1332-2）÷7+1=191项；从右向左数第191项的大数为：1333-（191-1）×4=573，小的数为：1+（191-1）×3=571，573-571=2.所以最小差为2。

　　四年级

　　1. 如图，这是一个用若干块体积相同的小正方体粘成的模型。把这个模型的表面（包括底面）都涂上红色，那么，把这个模型拆开以后，有3面涂上红色的小正方体比有2面涂上红色的小正方体多多少块？

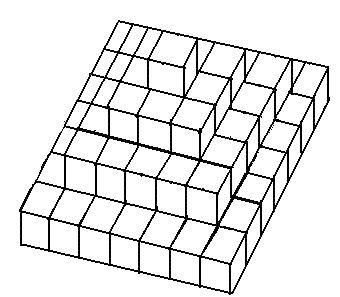
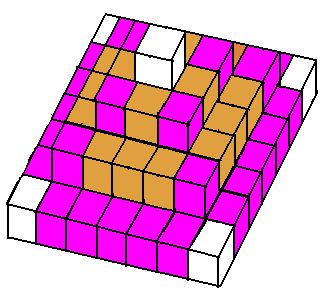
　　解答

　　3面红：1层有5×4=20（个），2层有4个，3层有4个，共20+4+4=28（个）

　　2面红：2层有3×4=12（个），3层有4个，共12+4=16（个）

　　3面红比2面红的多28-16=12（个）

　　2. 四个足球队进行单循环比赛，每两个队要赛一场。如果踢平，每队各得1分，否则胜队得3分，负队得0分。比赛结果，共出现4场平局，各队的总得分恰好是四个连续自然数。输给第一名的队的总分是多少？

　　解：4个队一共比赛3＋2＋1=6场。一共产生了2×3＋4×（1+1）=14分。14=2＋3＋4＋5

　　5分的：3+1＋1（一胜2平）

　　4分的：3+1＋0（一胜1平1负）

　　3分的：3+0＋0=1+1+1（一胜2负）（不可能，因为有3胜对4负。或平局是7场，不为偶）所以只能为（三平）

　　2分的：1+1＋0（一胜2平）。

　　得4分的一定胜了得2分的。所以得5分的一定打败了得4分的。

　　答：输给第一名的队总分是4分。

　　五年级

　　1. 某个自然数是3和4的倍数，包括1和它本身在内共有10个因数，那么这个自然数是几?

　　解答：这个自然数是48.

　　10＝2×5＝（1＋1）×（4＋1），4＝22，所以只能是3×24＝48.

　　2. 两个整数A，B的最大公因数是C ，最小公倍数是D，已知C不等于1，也不等于A或B，并且C＋D＝187，求A＋B是多少？

　　解答：A＋B＝119。

　　最大公因数C，当然最小公倍数D 的因数，C是187的因数。187＝11×17/

　　如果C＝11，就有D＝176，A和B都是176的因数，但A和B不能与C相同，只能是22，44，88，176。其中任意两个数的最大公因数都不是C＝11。

　　只有C＝17，D＝170，A和B是170的因数，又要是17的整数倍，有34，85，170三个数。只有34，85的最大公因数是C＝17。