北京市奥校精选试题及答案212

　　以下是北京市奥校内部试题，每套试题附有答案及详解。小升初目标校为东城区5中、2中的同学们要尤其注意此套试题。

　　二年级

　　1. 有1枚5分硬币、4枚2分硬币和8枚1分硬币，要拿出8分钱，共有多少种拿法？

　　解答：7种（列表法）

　　2. 学校食堂今天午餐的菜谱上有2个肉菜和2个素菜，小民想买一个肉菜和一个素菜。问共有几种不同的搭配方法？

　　解答：2×2=4（种）

　　三年级

　　1、有5个数,其平均数为138,按从小到大排列,前3个数的平均数为127，,后3个数的平均数为148,则第三个数是多少？

　　解答：设这5个数为、b、c、d、e。

　　a+b+c+d+e =690

　　a+b+c=381

　　则d+e=309

　　c+d+e=444

　　则c=135

　　2、大卡车一次能运7吨土，小卡车一次能运4吨土。现在有大、小卡车70辆，一次恰好能运土400吨。问大卡车有多少辆？

　　解答：（400–70×4）÷（7–4）=40（辆）

　　四年级

　　1. 甲乙二人在操场的400米跑道上练习竞走，两人同时出发，出发时甲在乙后面，出发后6分钟甲第一次超过乙，22分钟甲第二次超过乙。假设两人的速度保持不变，问：出发时甲在乙后面多少米？

　　解答： 150米

　　出发后，甲从第一次超过乙到第二次超过乙，用时22－6＝16（分）；

　　第二次超过的路程差为一圈400米，甲每分钟比乙多走400÷16＝25（米）；

　　第一次超过的追及路程25×6＝150（米）。

　　2. 甲、乙二人练习跑步，若甲让乙先跑10米，则甲跑5秒可追上乙；若乙比甲先跑2秒，则甲用4秒能追上乙。问：甲乙二人每秒各跑多少米？

　　解答：甲6米，乙4米

　　由第一次得甲乙二人速度差为每秒10÷5=2（米）；

　　由第二次得乙先跑的距离为2×4=8（米），乙每秒跑8÷2=4（米）

　　甲每秒跑4+2=6（米）。

　　五年级

　　1. 小明总是在上午9点乘学校来接的汽车去上学。有一天，汽车仍按以前的时间去接教授，而教授在上午8点15分就开始步行去上班，途中遇到接他的汽车，便立刻上车驶向学校，因此，这天小明比往常提前10分钟到校，那么汽车的速度是小明步行速度的几倍？

　　解答：学生的行走造成总时间节省了10分钟，也就是说小明走的路程汽车只需要

　　10÷2=5分钟，说明两人相遇时间是8:55分，此时小明共行走了40分钟，40÷5=8

　　2. 甲乙两班学生上午8：00出发距学校27千米的某地参观，有一辆汽车，每次只能坐一个班的学生，为了使两个班同时到达，要合理安排步行和乘车，若步行速度为4千米/小时，汽车速度60千米/小时，那么两班最早几点几分同时到达？

　　解答：全程就是8＋1＝9份。因此，每份是27／9＝3千米。

　　从图上可以看出，汽车行驶的总路程是8＋7＋8＝23份，所用时间就是：　3＊23／60＝1又3／20小时＝1小时9分　　所以，两个班最早9点9分同时到达。

　　六年级

　　1. 对于自然数1，2，3，…，100中的每一个数，把它非零数字相乘，得到100个乘积（例如23，积为2×3=6；如果一个数仅有一个非零数字，那么这个数就算作积，例如与100相应的积为1）．问：这100个乘积之和为多少?

　　解答：从1，2，…，9， 的乘积的数字和是45；

　　从11，12，…，19 的乘积的数字和是1×45；

　　从21，22， …，29， 的乘积的数字和是2×45，

　　…，

　　从91，92，…，99， 的数字和是9×45；

　　而10，20，…，90， 的数字和是45，

　　100的为1，故，其总和为：

　　（1＋1＋2＋3＋…＋9＋1）×45＋1＝47×45＋1＝2116

　　2.  一座石台的下底面是边长为10米的正方形,它的一个顶点A处有一个虫子巢穴,虫甲每分爬6厘米,虫乙每分爬10厘米,甲沿正方形的边由A→B→C→D→A不停的爬行,甲先爬行2厘米后,乙沿甲爬行过的路线追赶甲,当乙遇到甲后,乙就立即沿原路返回巢穴,然后乙再沿甲爬行过的路线追赶甲……在甲爬行的一圈内,乙最后一次追上甲时,乙爬行了_______分时间

　　解答：见下表,其中“乙下次要比甲多爬行的路程”=“甲已爬行路程”×2.

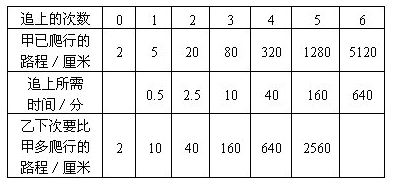
　　由上表看出,第 6次追上时,甲已爬行一圈多了,所以最后一次是第 5次追上,此时,乙共爬行0.5+2.5+10+40+160=213(分).