北京市奥校精选试题及答案232

　　以下是北京市奥校内部试题，每套试题附有答案及详解。小升初目标校为东城区5中、2中的同学们要尤其注意此套试题。

　　二年级

　　1．甲乙两个工程队合修一条长24千米的公路，修完后甲队比乙队多修4千米，甲队修了多少千米？乙队修了多少千米？

　　解答：（24+4）÷ 2 = 14（千米）——甲队

　　24 – 14 = 10（千米）——乙队

　　2．小明在一次测验中，语文和数学的平均分是96分，语文比数学少8分。语文得多少分？数学得多少分？

　　解答：96×2=192（分）

　　（192 + 8）÷ 2 = 100（分）——数学

　　192 – 100 = 92（分）——语文

　　三年级

　　1、在四位数8561的某一位数码后面再插入一个该数码，能得到的五位数最小是多少？

　　解答：85561

　　2、12张乒乓球台上共有34人在打球，那么正在进行单打和双打的台子各有多少张？

　　解答：利用鸡兔同笼的想法，假设都在进行单打，那么应有12×2=24人，多出34－24=10人。把单打变为双打，每个台子需要增加2人，所以双打的台子有10÷2=5张，单打的台子有12－5=7张。

　　四年级

　　1、有1克、2克、4克、8克和16克的砝码各一个，从这五个砝码中，每次任选两个使用和一架天平可称出多少种不同重量？

　　解答：方法一：由条件可知，可以称出的重量最少为1克，最重的重量为8+16=24克。再通过枚举，可知，11克、13克、16克、19克、21克、22克和23克无法称出，其它整克数均可称出，故共可称出17种不同的重量。

　　方法二：五个砝码选两个称重可以有2× =20种方法，但是，16-4=8+4、8-2=2+4,4-1=2+1重复出现，因此一共有17种不同的重量。

　　2、19+199+1999+19999+199999=

　　解答：原式=222215

　　五年级

　　1、 将1～8这八个数分别填入右图的○中，使两个大圆上的五个数之和都等于21。

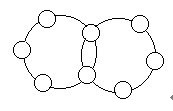
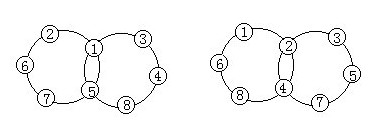
　　分析与解：中间两个数是重叠数，重叠次数都是1次，所以两个重叠数之和为　　21×2-(1+2+…+8)=6。在已知的八个数中，两个数之和为6的只有1与5，2与4。每个大圆上另外三个数之和为21-6=15。如果两个重叠数为1与5，那么剩下的六个数2，3，4，6，7，8平分为两组，每组三数之和为15的只有2+6+7=15和3+4+8=15，

　　故有下左图的填法。如果两个重叠数为2与4，那么同理可得下右图的填法。

　　2、将1～6这六个自然数分别填入图中的六个圈中，使得三角形每条边上的三个数之和都相等。

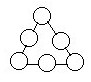
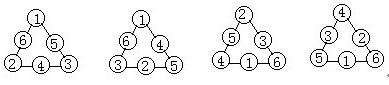
　　分析与解：与例2不同的是不知道每边的三数之和等于几。因为三个重叠数都重叠了一次，由(1+2+…+6)+重叠数之和M=每边三数之和K×3，得到每边的三数之和K

　　K=[(1+2+…+6)+M]÷3=(21+M)÷3=7+M÷3。

　　因为每边的三数之和是整数，所以重叠数之和M应是3的倍数。考虑到重叠数是1～6中的数，所以三个重叠数之和M只能是6，9，12或15，对应的每条边上的三数之和就是9，10，11或12。与例2的方法类似，可得下图的四种填法：K1=9 ，k2=10，k3=11，k4=12