北京市奥校精选试题及答案236

　　以下是北京市奥校内部试题，每套试题附有答案及详解。小升初目标校为东城区5中、2中的同学们要尤其注意此套试题。

　　二年级

　　1．三个物体平均重量是31千克，甲物体比乙、丙两个物体重量之和轻1千克，乙物体比丙物体重量的2倍还重2千克，三个物体各重多少千克？

　　【解答】   31 × 3= 93（千克）——三个物体重量总和

　　（93 + 1）÷ 2 = 47（千克）——乙、丙重量之和

　　47 - 1 = 46（千克）——甲的重量

　　（47 – 2）÷ 3 = 15（千克）——丙的重量

　　15 × 2 + 2 = 32（千克）——乙的重量

　　2．甲、乙两个工程队共198人，甲队为了支援乙队，抽出28人调入乙队，这时乙队人数还比甲队少2人，求甲乙两队原有工人多少人？

　　【解答】   （198+ 2）÷ 2 = 100（人）

　　100– 2 – 28= 70（人） ——乙队人数

　　100 + 28  = 128（人）——甲队人数

　　三年级

　　1、把16分成几个互不相等的自然数的和，再求这些数的积，要使乘积最大，则这个乘积的算式是什么？

　　解答：16=2+3+5+6 最大乘积则是2×3×5×6

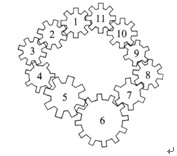
　　2、平面上有11个齿轮咬合成一圈．试问，能否使这些齿轮同时转动起来？

　　解答：不能。假设齿轮1顺时针转动，则齿轮2就应当逆时针转动，齿轮3应当顺时针转动，齿轮4应当逆时针转动……。显然，凡“奇数号”齿轮均应顺时针转动，而“偶数”号均应逆时针转动．这样一来，齿轮1和齿轮11均为顺时针转动，这是不可能的。

　　四年级

　　1、四个人互相传球，由甲开始发球，并作为第一次传球，要求每两人之间最多只做过一次传接，若满足以上要求最多可传球多少次？

　　解答：由于每两人之间可以传球一次，故可以传球3×4÷2=6次。但是要求每两人之间最多可以传球一次，由一笔画问题可知，4人中只能有2人传球的次数是奇数，因此要去掉一次传球。故最多可以传球5次。

　　2、直角三角形的斜边长是6，面积是7，那么这个直角三角形的两条直角边的和是（   ）。

　　解答：不能。假设齿轮1顺时针转动，则齿轮2就应当逆时针转动，齿轮3应当顺时针转动，齿轮4应当逆时针转动……。显然，凡“奇数号”齿轮均应顺时针转动，而“偶数”号均应逆时针转动．这样一来，齿轮1和齿轮11均为顺时针转动，这是不可能的。

　　四年级

　　1、四个人互相传球，由甲开始发球，并作为第一次传球，要求每两人之间最多只做过一次传接，若满足以上要求最多可传球多少次？

　　解答：由于每两人之间可以传球一次，故可以传球3×4÷2=6次。但是要求每两人之间最多可以传球一次，由一笔画问题可知，4人中只能有2人传球的次数是奇数，因此要去掉一次传球。故最多可以传球5次。

　　2、直角三角形的斜边长是6，面积是7，那么这个直角三角形的两条直角边的和是（   ）。

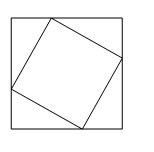
　　解答：将四个这样的直角三角形拼成一个正方形，可得正方形的面积为6×6+4×7=64，因此，这个直角三角形的两条直角边的和是8.

　　五年级

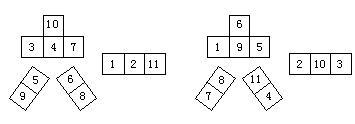
　　1、将1～11这11个数分别填入图11中的方格内，每个数只许用一次，使每行或列（斜列）中的所有方格内数的和都相等。

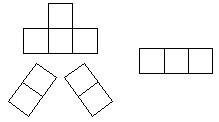
　　分析与解：设中心数为a，每行或列所有方格内数的和为k

　　k是整数，a可能是4或9。

　　当 时，

　　当 时，

　　可得到两个基本解，见下图。

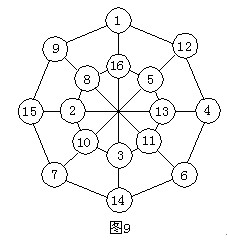
    2、将1—16这16个数分别填入图8的16个○内，使每条线段上四个○内数的和相等，两个八边形八个顶点上○内数的和也相等。