北京市奥校精选试题及答案253

　　以下是北京市奥校内部试题，每套试题附有答案及详解。小升初目标校为东城区5中、2中的同学们要尤其注意此套试题。

　　三年级

　　1. 一个长方形的周长是22米，如果它的长和宽都是整米数，那么这个长方形的面积有多少种可能？

　　【解析】共5种。

　　由于长方形的周长是22米，可知它的长与宽之和为11米。下面列举出符合这个条件的各种长方形：1×10=10   2×9=18   3×8=24  4×7=28  5×6=30

　　2．把15个相同的玻璃球分成数量不同的4堆，共有多少种不同的分法？

　　【解析】共有6种不同的分法。

　　15 = 1+2+3+9 = 1+2+4+8 = 1+2+5+7 = 1+3+4+7 =1+3+5+6 =2+3+4+6

　　四年级

　　1、师生共720人外出参观。一辆大客车比一辆面包车多载20人，6辆大客车和8辆面包车载的人数相等。如果都乘面包车需要几辆？如果都乘大客车需要几辆？

　　【解答】20×6=120，120÷（8-6）=60（人），720÷（60+20）=9辆大客车；

　　720÷60=12辆面包车；

　　2、师生共100人去植树，教师每人栽3棵树，学生平均每3个人栽1棵，一共栽100棵，教师和学生各有多少人？

　　【解答】3×3-1=8（棵）100×3=300（棵），300-100=200（棵），200÷8=25（组）

　　学生：25×3=75（人） 老师：100-75=25（人）。

　　五年级

　　1、每次用1，1，2，2，3，3六个数字可以组成多少个不同的六位数？

　　答案：6! ÷2! ÷2! ÷2!=90

　　2、有4个相同的白球和6个相同的黑球排成一排，要求4个相同的白球两两不相邻，有多少种排列方式？

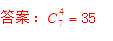
　　六年级

 

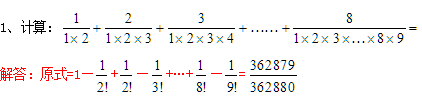
　　2、现有11人在一起聚会，每个人至少认识其中的一个人。如果仅有两个人所认识的人数相同，那么这两个人中的每一个人所认识的人数是多少？

　　解答：由于“仅有两个人所认识的人数相等”所以11人分别认识的人数应该有而且也只能有10种情况，即所认识的人数为1人到10人。设分别认识1，2，3，…10人的人分别A1，A2，A3，…A10的人。我们可以从认识10人的A10开始逆推，显然A1再不可能被别人认识；接下来A9，则A2也不可能被他人认识；以此类推，考虑A6 ，则A5也再不可能被他人认识了。最后，对于A11的人，能而且只能并且必须认识其中A6到A10的5个人，因此，这两个认识所认识的人数是5。