小升初奥数天天练数论——整除之拆分

    北京奥数网讯 智康1对1付金海老师每日提供奥数天天练试题供咱们小升初的孩子练习，今日发布数论——整除之拆分。

    点击进入：奥数天天练

　　考点：整除拆分

　　难度：4星

　　来源：思维导引

　　题目：在1、2、3、4……2007这2007个数中有多少个自然数a能使2008+a能被2007-a整除。

　　答案：本题考察代数知识的综合技巧，是一道难度较大的题目。要使得2008+a能被2007-a整除，我们可以将条件等价的转化为只要让是一个整数即可。下面是一个比较难的技巧，我们知道若a可以使得是一个整数，那么a也同样可以使得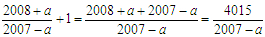是一个整数，这样只要2007-a是4015的约数即可，将4015分解可知其共有8个因数，其中4015是最大的一个，但是显然没有可以让2007-a等于4015的a的值，其余的7个均可以有对应的a的值，所以满足条件的a的取值共有7个。

　　分析：此题曾被一些学校用做升学考试题目，难度较大，同时也借用了代数知识，转换为数论的约数倍数问题。华杯赛中也出现过类似题目：求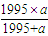是整数，其方法是一样的。由于分子、分母同时还有未知数，我们第一要解决的问题就是只让其中之一含有未知数，从而想到利用+1来解决问题，对于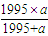我们可以利用+1995来解决。