北京市奥校精选试题及答案89(2)

　　二年级

　　1. 仔细观察，找出变化规律，想一想横线处应填什么图形？

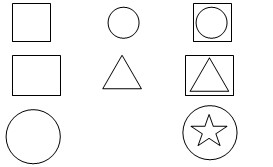
　　解答：是五角星。前两个图形结合起来就是第三个图形。都是外边图形套着里边图形。

　　2. 用○、★、△代表三个数，有○＋○＋○＝15，★＋★＋★＝12，△＋△＋△＝18，○＋★＋△＝？

　　解答：上面算式中的○、★、△分别代表三个数，根据三个相同加数的和分别是15、12、18，可知○＝5，★＝4，△＝6，又5＋4＝6＝15，所以应是15。

　　三年级

　　1. 在一个停车场上，现有车辆24辆，其中汽车有4个轮子，摩托车有3个轮子，这些车共有86个轮子，那么三轮摩托车有多少辆？

　　解答：假设都是三轮车，应有3×24＝72个轮子，少了86－72＝14个轮子。

　　每把一辆汽车假设为三轮车，会减少4－3＝1个轮子。

　　汽车有：14÷1＝14（辆）；从而求出三轮车有24－14＝10（辆）。

　　2. 现有形状完全相同的硬币18枚，已知其中有一枚假币，假币比真币要轻，现有一台无砝码的天平，则至少要称多少次，才能找出这枚假币？

　　解答：可以这样来找出假币：首先将18枚硬币分成A、B、C三组，每组6枚硬币。先将A，B两组硬币分别放在天平两边，这样可以确定假币在哪一组。比如A比B轻，则假币在A中；如A比B重，则假币在B中；如A、B一样重，则假币在C中。

　　不妨设假币在A中，再将A中的六个硬币分成a、b、c三组，每组两个硬币。同理假设在a组，此时再称一次即可找出假币，这样通过3次称量即可找出假币。

　　四年级

　　1. 一次象棋比赛，进行循环赛（每位选手都与其他选手赛一场），赢者得2分，负者得0分，平局两人各得1分。现有四人统计选手总分分别为89分、90分、92分、93分，但只有一人统计正确，问共有多少位选手？

　　解答：不管有几位选手赛多少场，每一场的得分总数是2分，所以统计选手总分应是2的倍数。故排除89分和93分。

　　再看90分和92分分别赛几场的总分  90÷2＝45（场）    92÷2＝46（场）

　　场数能写成从1开始的自然数的和。只有45＝1＋2＋3＋4＋5＋6＋7＋8＋9

　　所以正确的总分是90分。每位选手共赛9场，一共有10位选手。

　　2. 猴妈妈给孩子们分桃子，第1只小猴子分到1个，第2只小猴子分到4个，第3只小猴子分到7个，第4只小猴子分到10个，……。按照这样的方法分下去，猴子淘淘排在第30名，它着急地问：“我能分到多少个桃子呢？”聪明的同学们，请你帮它算一算？

　　解答：每个猴子分到的桃子数，构成了一个等差数列。1＋（30-1）×3＝88（个）

　　五年级

　　1. 把下面的十进制数转化为二进制数。15、128、34

　　解答：(15)10＝(1111)2       (128)10＝(10000000)2      (34)10＝(100010)2

　　2. 把12名同学分成6组，使每组恰有两名同学，共有多少种分法？

　　解答： ＝10395（种）

　　六年级

　　1. 重阳节某社区开展尊老敬老活动，邀请老年人和小朋友一起去秋游。参加这次秋游的老年人有25人，小朋友20人，另外有3名工作人员。公园的门票规定：成人每人30元，学生每人15元，30人以上（包括30人）可以购买团体票，团体票每人20元。请你设计一种最合理的购票方案，这种购票方案只用多少元？

　　解答：尽量让成年人买团体票，让小朋友买学生票。25名老年人，3名工作人员，再加2名小朋友共30人，购买团体票需要20×30＝600（元）；剩下18名小朋友，购买学生票共用18×15＝270（元），所以这种购票方案只用600＋270＝870（元）。

　　2. 在1至2009（含2009）的所有正整数中，数字和能被5整除的数共有多少个？

　　解答：在0000—1999这2000个数中，前三位有000、001、002、……198、199共有200种取值，现在用ABC来表示。

　　当ABC配上个位数字0—9后，由于0—9除以5的余数依次为0、1、2、3、4、0、1、2、3、4，于是无论A＋B＋C除以5的余数为多少时，所构成的四位数中有且只有两个数的数字之和能被5整除，故0000—1999这2000个数中，有200×2＝400个数的数字之和能被5整除。又因为0000的数字之和能被5整除，所以0001—1999中有400－1＝399个数的数字之和能被5整除。又2000—2009这10个数中，只有2003和2008的数字之和能被5整除。所以1—2009中数字之和能被5整除的有399＋2＝401（个）。