北京市奥校精选试题及答案102(2)

　　二年级

　　1.有一棵古树，树上挂着一个牌子，牌子上写着：要问我今年多少岁，100比我小，1000比我大，从左往右每位数字增加2，各位数字之和是21。那么这棵树今年多少岁？

　　解答：年龄肯定是个三位数，通过数字和是21可以判断出21=5＋7＋9，因此这棵树今年579年。

　　2.图中相当于一个棋盘，警察先走，双方交替走棋，每次只能沿着线走一步。那么警察至少需要走多少步才能抓住小偷？

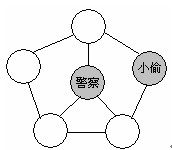
　　解答：警察第一步走到B，小偷为躲避警察只能走到D。

　　警察第二步走到A，小偷只能走到C。

　　警察第三步走到F，小偷只能走到D或B。

　　警察第四步就能抓到小偷。

　　三年级

　　1.小明的口袋中有一元、二元、五元、十元、五十元、一百元的纸币各一张。如果每次取出5张计算它们的钱数总和，共有多少种不同的总和？

　　解答：一共6张，每次取5张，剩下一张，所以从剩下的钱数考虑，剩下的那张共有6种可能。每次取出5张的钱数总和可以用所有钱的总和减去剩下那张的钱数。由于每张钱的钱数都不一样，因此取出的5张钱数总和也肯定各不相同，所以共有6种不同的总和。

　　2.在一次大队长选举中，五位候选人共获得320张选票，获胜者比其他四位分别多得9、13、18、25张选票，那么获得票数最少的候选人获得多少张选票？

　　解答：如果其他四位分别加上9、13、18、25张选票，他们的得票数就和获胜者一样了。因此获胜者的得票数为（320＋9＋13＋18＋25）÷5=77张，获得票数最少的人的得票数为77－25=52张。

　　四年级

　　1.爱尔兰作家刘易斯曾写过一篇反讽寓言，文中描述了一个名为尼亚特泊的野蛮国家。在这个国家里使用西巴巴数字。西巴巴数字的形状与通用的阿拉伯数字相同，但含义相反。如“0”表示“9”，“1”表示“8”，以此类推。他们写数字是从左到右，使用的运算符号也与我们使用的一样。例如，他们用62代表我们所写的37。按照尼亚特泊人的习惯，837＋742的计算结果是多少？

　　解答：837就是阿拉伯数字中的162，742就是阿拉伯数字中的257，162＋257=419，419用尼亚特泊人的习惯写就是580，因此计算结果是580。

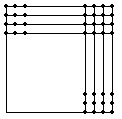
　　2.用一堆围棋子围成一个实心方阵，余下18个。如果横纵各增加4排，摆成的新正方形还需要追加62个，那么最初有多少个棋子？

　　解答：横纵增加4排后，共增加了18＋62=80个。如图，右上角有4×4=16个棋子既在横排又在纵排，去掉这16个后，横纵每排棋子就一样多了，每排有（80－16）÷8=8个。原来的正方形就是8×8的，原有棋子8×8＋18=82个。

　　五年级

　　1.甲、乙两车分别从A、B两地同时相向开出，已知甲车速度是乙车的1.5倍。A、B两地中间有一C地，甲、乙分别通过C地的时刻为5点整和15点整。那么甲、乙两车相遇是在什么时刻？

　　解答：设乙速为“1”，甲速就是1.5。当甲到达C地时，乙还差15－5=10个小时的路程，那么这段路程就是1×10=10。这时甲乙相距的距离也就是10。10÷（1＋1.5）=4（小时），说明再过4个小时甲乙可以相遇，那么相遇的时刻就是5＋4=9点整。

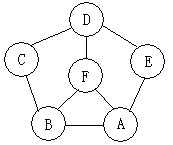
　　2.两人轮流在图中涂色，已经涂过的地方和其相邻的地方就不能再涂。例如，甲先涂A，乙涂E，甲就再没有可涂的地方，甲就输了。如果先涂者要想取胜，那么应该先涂哪个地方？

　　解答：先涂者可以先涂D。

　　通过试验可以知道，如果涂其它地方，那么剩下可涂的部分都是相邻的几块，后涂者一定会有办法使得先涂者无法再涂。而如果先涂者涂D，那么B、C、E、F就没法再涂了，只有A和G可以涂。而A和G不相邻，无论后涂者涂哪块，先涂者都可以涂另外一块，使得后涂者无法再涂。

　　六年级

　　1.图中是一个等腰三角形的螺旋。每个三角形中的最大角是100°。灰色三角形的编号是0，余下的三角形的编号依次是1、2、3、……。它们是在前一个三角形的一条边上形成的。从图中可以看出，3号三角形只部分地覆盖了0号三角形，那么第一个完全覆盖0号三角形的三角形编号是多少？

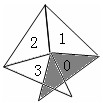
　　解答：一周为360°，三角形每转一次是100°，[360，100]=1800，所以必须转1800°才能第一次转回原处。1800÷100=18（次），也就是编号为18的三角形会与0号三角形重合。

　　2.正方形折纸先对折一次，找到中央折线。然后如图，将折纸的一个角折到中央折线上，那么∠ABE是多少度？

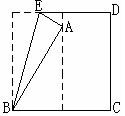
　　解答：将D点折到中央线也会落在A点，因此三角形ABC为等边三角形，即∠ABC是60°，那么∠ABE=（90°－60°）÷2=15°。