北京市奥校精选试题及答案105(2)

　　二年级

　　1.下面有5组图形，每个各有5个小正方形，请把这5个图形拼成一个大正方形，可以怎样拼？

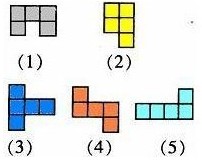
　　解答：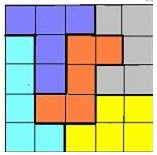

　　2.参加朗诵的男生共10人，他们站成一排，要在每相邻两个男生之间插入一个女同学，这时一共有多少名同学？

　　解答：10个男生中间有9个间隔，可以插入9个女生，共有10＋9=19名同学。

　　三年级

　　1.如果1个笔记本的价钱等于5块橡皮的价钱，4个文具盒的价钱等于40块橡皮的价钱。已知1个笔记本的价钱是3元，那么1个文具盒的价钱是多少？

　　解答：5块橡皮的价钱是3元，40块橡皮的价钱是3×（40÷5）=24元，1个文具盒的价钱是24÷4=6元。

　　2.学校买来白粉笔比彩粉笔多15箱，白粉笔的箱数比彩粉笔的4倍少3箱，学校买来的白粉笔和彩粉笔各多少箱？

　　解答：如果白粉笔增加3箱，那么白粉笔就是彩粉笔的4倍，这时比彩粉笔多15＋3=18箱。彩粉笔的箱数是18÷（4－1）=6箱，白粉笔实际有6＋15=21箱。

　　四年级

　　1.有四个互不相等的自然数，最大数与最小数的差等于4，最小数与最大数的乘积是一个奇数，而这四个数的和是最小的两位奇数。求这四个数。

　　解答：这四个数的和是11，最大数与最小数都是奇数，而其它两个数应该是一奇一偶。如果最小数是1，那么最大数就是5，另两个数只能是2和3。如果最小数是3，最大数是7，那么肯定不满足。所以这四个数分别是1、2、3、5。

　　2.桌子上有6只开口向上的杯子，每次同时翻动其中的5只杯子，问能否经过若干次翻动，使得全部杯子的开口全部向下？

　　解答：要想使杯子开口从向上变为向下，那么每个杯子都需要进行奇数次翻动，即1次或3次或5次……。6只杯子，每只杯子进行奇数次翻动，一共就需要进行偶数次翻动，而每次操作可以翻动5只杯子，所以只要进行偶数次操作就可以。构造如下：第一次翻动1、2、3、4、5号，第二次翻动2、3、4、5、6号，第三次翻动3、4、5、6、1号，第四次翻动4、5、6、1、2号，第五次翻动5、6、1、2、3号，第六次翻动6、1、2、3、4号。

　　五年级

　　1.下面是某一湖泊的平面图，图中所有曲线都是湖岸。（1）如果P点在岸上，那么A点是在岸上还是在水中？（2）某人过此湖泊，他下水时脱鞋，上岸时穿鞋。如果他从A点出发走到某点B，他穿鞋与脱鞋的总次数是奇数，那么B点在岸上还是在水中？为什么？

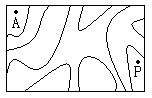
　　解答：可以将所有湖泊的部分用蓝色标注，如图。

   

　　（1）很容易反现A在水中。

　　（2）从A点出发，那么此人现在的状态是脱鞋。他先要上岸穿鞋，然后再脱鞋入水，再上岸穿鞋，再脱鞋入水，所以第1、3、5、……次他一定是上岸穿鞋，即经过奇数次后他一定是在岸上，所以B在岸上。

　　2.将1、4、7、10、13、16、19、22八个数分别填入圈内，如果正方形每条边上的三个数的和都相等，那么四个角上的四个数的和最小是多少？

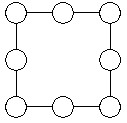
　　解答：1＋4＋7＋10＋13＋16＋19＋22=92，每条边的和都一样，那么92与四个角上的数的总和应该是4的倍数，而92是4的倍数，所以要求四个角上的数的和也是4的倍数。这四个数的和最小为1＋4＋7＋10=22，不是4的倍数，如果再增加的话，至少增加3，所以22＋3＋3=28是4的倍数。

　　那么四个角上的数之和是28能不能成立？构造如下：

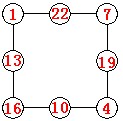
　　28=1＋4＋7＋16

　　六年级

　　1.将六分之一表示成两个自然数的倒数之和，有多少种表示方法？请给出所有的答案。

　　2.下图所示的这块木板可看成由五个小正方形组成。聪明的木工只锯了两次，就评出了一个正方形桌面。想一想，他是怎样锯、怎样拼的？

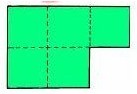
    解答：