北京市奥校精选试题及答案113(2)

　　二年级

　　1.找规律，在？处填入适当的数。

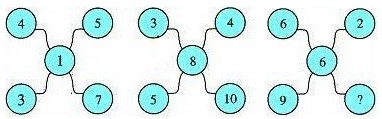
　　解答：上面两个数的和加上中间的数等于下面两个数的和。？处应该是6＋2＋6－9=5。

　　2.用16根火柴棒可以摆成4个正方形（如图），那么减少1根火柴后，用15根火柴棒还可以摆成4个正方形，应该怎样摆法？

　　解答：

　　三年级

　　1.请你移动期中的一根火柴棒，使等号两边相等。

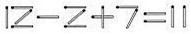
　　解答：2＋2＋7=11

　　1.裁缝有一段16米长的布，每天剪去2米，第几天剪去最后一段？

　　解答：16÷2－1=7（天）

　　四年级

　　1.把50枚黑棋子排列在正五边形的五条边上，每条边上的黑棋子个数相等，且每个角上有一枚，然后在所有相邻的两枚黑棋子间放两枚白棋子。问：每条边上的黑、白棋子共有多少枚？

　　解答：50枚黑棋子中间一定会插入50枚白棋子，这样一共有100枚棋子。五边形每个角上的黑棋子会被重复计算，所以每条边上有（100＋5）÷5=21枚。

　　2.3件运动衣上的号码分别是1，2，3，甲、乙、丙3人各穿一件。现有25个小球，首先发给甲1个球，乙2个球，丙3个球。规定3人从余下的球中各取球一次，其中穿1号衣的人取他手中球数的1倍，穿2号衣的人取他手中球数的3倍，穿3号衣的人取他手中球数的4倍，取走之后还剩下两个球，那么，甲穿的运动衣的号码是多少？

　　解答：总数25个，先把开始分给甲，乙，丙的球数还要剩下的球数减去，算出剩25－1－2－3－2=17（个）。也就是把17个球再分发出去，试一试，谁的1倍＋谁的3倍＋谁的4倍=17，2×1＋1×3＋3×4=17，说明是1个球的3倍，所以甲是穿2号。

　　五年级

　　1.两人轮流数数，每人每次可以数1个或2个或3个，但是不能不数，例如第一个人数1，2，第二人可接着往下数，他可以数到3，也可以数3，4，也可以数3，4，5，如此继续，谁数到100，谁就算胜。请试一试，谁有必胜策略？

　　解答：无论先数的那个人数几个数，后数的人总会有办法使得自己正好数到4、8、12、……，也就是说后数的人每次都能数到4的倍数，而先数的人数不到，所以后数的人必胜。

　　2.AB两地相距65千米，甲、乙骑车从A地，丙骑车从B地同时出发相向而行。甲、乙、丙的骑车速度分别是每小时10、12、15千米。出发后多少小时后丙正好在甲、乙的正中间，即丙与甲、乙的距离相等？

　　解答：根据三人的速度可知，当丙正好在甲乙中间时，甲走了10份的路程，乙走了12份的路程，丙走了15份的路程。由于丙在甲乙正中间，所以丙距离A地应该正好还有11份的路程，所以全程共有11＋15=26份的路程，每份路程为65÷26=2.5千米。甲共走了10份路程，即25千米，甲速为每小时10千米，所以时间为25÷10=2.5小时。

　　六年级

　　1.原计划用24个工人挖一定数量的土方，按计划工作5天后，因为调走6人，于是剩下的工人每天比原定工作量多挖1方土才能如期完成任务，原计划每人每天挖土多少方？

　　解答：调走6人还剩18人，那么18个人还干24个人的活，即3个人干4个人的活，每个人要多干三分之一个人的活，因此三分之一个人要挖1方土，所以每个人要挖3方土。

　　2.如图：已知平行四边形ABCD的面积为12，M为BC的中点，图中阴影部分的面积是多少？

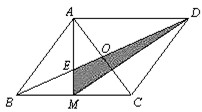
　　解答：M为中点，所以三角形MCD的面积为12÷4=3，梯形ABMD的面积就是12－3=9。观察这个梯形发现，AD=2BM，即上下底的长度比为1:2，因此三角形BEM、ABE、EMO、ADE的面积比为1:2:2:4，阴影部分面积为9÷（1＋2＋2＋4）×2=2。