北京市奥校精选试题及答案290(2)

　　二年级

　　1、 用○、★、△代表三个数，有○+○+○=15，★+★+★=12，△+△+△=18，○+★+△=（   ）

　　分析：上面算式中的○、★、△分别代表三个数，根据三个相同加数的和分别是15、12、18，可知○=5，★=4，△=6，又5+4+6=15，所以（  ）内应填15。

　　2、 仔细观察，找出变化规律，想一想空格里应填什么图形？

　　答案：是□○△ 。可以横着、竖着、斜着观察。

　　三年级

　　1、妈妈今年35岁，恰好是女儿年龄的7倍。（ 10 ）年后，妈妈的年龄恰好是女儿的3倍。

　　35÷7=5（岁）  （35-5）÷（3-1）=15（岁）  15-5=10（年）

　　2、赵、田、钱、李、吴五位老师，赵老师比田老师大4岁，钱老师比赵老师大3岁，李老师比赵老师

　　小3岁，吴老师比钱老师小2岁.这五位老师的年龄加在一起是122岁.问：五位老师各多少岁？

　　解题时先确定以赵老师年龄为标准量.

　　赵老师年龄的五倍：122+ 4-3+3-1=125（岁）

　　赵老师年龄：125÷5=25（岁）

　　田老师年龄：25- 4= 21（岁）

　　钱老师年龄：25+ 3= 28（岁）

　　李老师年龄：25- 3= 22（岁）

　　吴老师年龄：25+ 1= 26（岁）

　　四年级

　　1、天天带了一些苹果和梨到敬老院慰问。每次取出2个梨和5个苹果送给老人，最后当梨正好分完时，还剩下11个苹果。这时他才想起原来苹果是梨的3倍。原有苹果、梨各多少个？

　　答案：11÷（6－5）=11（次） 11×2=22（个）梨  22×3=66（个）苹果

　　2、某班共有30名男生，其中20人参加足球队，12人参加篮球队，10人参加排球队。已知没有一个人同时参加三个队，且每人至少参加一个队，有6人既参加足球队又参加篮球队，有2人既参加篮球队又参加排球队。那么既参加足球队又参加排球队的有多少人？

　　答案：20＋12＋10－2－6－30=4（人）

　　五年级

　　1、有一个直角梯形ABCD（图11），已知AB=8厘米，CD=4厘米，BC=6厘米，三角形ABF的面积比三角形EFD的面积大17.4平方厘米，那么ED长多少厘米？

　　

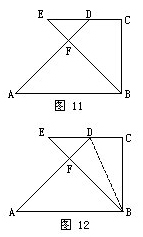
　　分析与解连接DB（图12）。已知三角形ABF比三角形EFD的面积大17.4平方厘米，所以三角形ABD比三角形BED的面积也大17.4平方厘米。已知 AB=8厘米，BC=6厘米，三角形ABD的面积等于8×6÷2=24（平方厘米）。三角形BDE的面积是：24-17.4=6.6（平方厘米）。而三角形 BDE的面积等于ED×BC÷2即ED×6÷2=6.6所以ED长是2.2厘米。

　　答：ED的长是2.2厘米。

　　2、图 24中四边形ABCD是一个正方形。E、F分别为CD和BC边上的中点。已知正方形ABCD的边长是30厘米，那么图中阴影部分的面积是多少平方厘米？

　　分析与解已知四边形ABCD为正方形，E、F分别为CD边与BC边上的中点，因此，三角形BCE和三角形DCF面积相等。这两个三角形的面积各自减去四边形 GFCE的面积，各自剩下的三角形GBF和三角形GDE面积还是相等的。连接GC（如图24），三角形GBF面积和三角形GCF的面积是相等的，因为这两个三角形等底同高。同理，三角形GCE面积和三角形GDE的面积也是相等的。而三角形GBF的面积和三角形GDE的面积相等，因此，三角形GBF、三角形 GCF、三角形GCE及三角形GDE是具有相等面积的四个三角形。

　　因为正方形ABCD面积等于三角形BCE的面积的4倍，所以图中空白部分的面积，即三角形GBF、三角形GCF、三角形GCE、三角形GDE的面积之和为正方形ABCD面积的1÷4÷3×4从而得出图中阴影部分的面积为正方形ABCD面积的2/3。

　　那么阴影部分的面积是：30×30×2÷3=600（平方厘米）

　　六年级

　　1、一项工程，甲单独干需要20天，乙单独干需要30天，现在由他们两人合干，又知甲在工作途中先请了3天事假，后因公事出差2天。求他们完成这项工程从开工到结束一共花了多少天？

　　解答：相当于乙单独干了5天，其余天数是甲乙合干的。1-5×1/30=5/6，5/6÷（1/30+1/20）=10（天），（10+5）=15天。

　　2、从1至25这25个自然数中，每次取出两个不同的数，使他们的和是4的倍数，共有多少种不同的取法？

　　解答：按除以4的余数分类：

　　（4，8，12，16，20，24）中任取2个：共15

　　（2，6，10，14，18，22）中任取2个：共15

　　（1，5，9，13，17，21，25）和（3，7，11，15，19，23）中各取1个：7×6=42

　　共有15+15+42=72种。